Ejournal 1: “Sequences and Series”

Why it is possible to solve for the sum of an infinite geometric series?

First of all, let's start off by defining an infinite geometric series. An infinite geometric series is the sum of an infinite geometric sequence. There wouldn't be a last term in this series. 

 The formula a1+a1r+a1r^2+a1r^3+…, where a1 is the first term and r is the common ratio, is the general pattern of the infinite geometric series.

It is possible to find the sum of all finite geometric series. Although in the case of an infinite geometric series when the common ratio is more than one, the terms in the sequence will only become bigger and bigger and if you add the larger numbers, there will be no final answer. The only possible answer would be infinity. So, we can only find the sum of the series when the common ratio greater than one for an infinite geometric series.

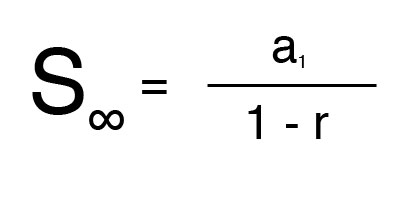
But, it is possible to get an answer because it converges (has a finite sum even when n is infinitely large). The sum of an infinite geometric series can be calculated as the value that the finite sum formula approaches as the number of terms n approaches infinity.

Relating “convergent and divergent” notes to “Sequences and Series”

In both ways of thinking, whether using imagination or logic, we have to use both when solving problems related to sequences and series. Mainly, convergent thinking is used as we have to analyze the question before answering it so that we can apply the right formula, but we also have to be creative in thinking as that type of problem might be the first you’ve encountered so we have to approach it with many ideas on how to solve it.

Real life application of Sequences and Series

1. Tumour growth, the growth rate is exponential except when it becomes so large that it cannot get food to grow effectively. So it starts off like an exponential graph but then stops completely. A more precise statement is known as Gompertz Law of Mortality – “rate of decay falls exponentially with current size”.
2. The Taylor series was used by Albert Einstein in his 1905 paper on Brownian motion to deduce the motion was the accumulated effect of momentum transfer from many individual atoms, thus proving their existence.

IB Learner Profile

The IB Learner Profile which best describes this eJournal is ‘Inquirers’ because I had to be curious and ask questions to research.

References:

https://www.varsitytutors.com/hotmath/hotmath_help/topics/infinite-geometric-series

http://www.nabla.hr/CO-SequAndSeries4.htm

3 Modes Of Thinking: Lateral, Divergent & Convergent Thought

3 Modes Of Thinking: Lateral, Divergent & Convergent Thought

3 Modes Of Thinking: Lateral, Divergent & Convergent Thought

3 Modes Of Thinking: Lateral, Divergent & Convergent Thought

https://www.teachthought.com/critical-thinking/3-modes-of-thought-divergent-convergent-thinking/

https://www.quora.com/What-are-the-applications-of-sequences-and-series